Discrete math:
digit (numbrimärk, цифра)
number (number, номер)
amount (arv, число)
Hardware:
data bus (andmesiin, шина данных)
address bus (aadressisiin, шина адреса)
control bus (juhtimissiin, шина управления)
Automation:
actuator (täitur, исполнительный механизм)
sensor /active/ (andur (tajur + signaali töötlemine),
датчик (сенсор + обработка сигнала))
controller (kontroller, контроллер)
0 -- pole
1 -- I 11 = 10 + 1 -- XI 50 -- L (legion)
2 -- II 12 = 10 + 2 -- XII 100 -- C (centurion)
3 -- III 13 = 10 + 3 -- XIII 500 -- D (division)
4 -- IV 14 = 10 + 4 -- XIV 1000 -- M (million)
5 -- V 15 = 10 + 5 -- XV
6 -- VI 16 = 10 + 6 -- XVI
7 -- VII 17 = 10 + 7 -- XVII
8 -- VIII 18 = 10 + 8 -- XVIII
9 -- IX 19 = 10 + 9 -- XIX
10 -- X 20 = 10 + 10 -- XX
Example:
1984 = 1000 + (-100+1000) + (50+30) + 4 -- MCMLXXXIV
Exercise 1: Build decimal to roman converter:
Exercise 2: Build roman to decimal converter:
We are using decimal system because we have 10 fingers
0 1 2 3 4 5 6 7 8 9 ... 10 11 ... 100 ... 1000
binary: we have only two digits 0 and 1
0 1 10 11 100 101 110 111 1000 1001
2021 = 11111100101
octal: binary numbers are too long for the human eye, so we pad a number with zeroes to the left side to make a number length dividable by 3 without reminder, then replace every triade with octal digits:
0 1 2 3 4 5 6 7 10 11 .. 17 20 ..
2021 = 011 111 100 101 = 3745
10 === --- === --- 8
3 7 4 5
hexadecimal: binary numbers are too long for the human eye, so we pad with zeroes to the left side to make a number length dividable by 4 without reminder, then replace every quartet with hex digits:
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 ..
2021 = 0111 1110 0101 = 7E5
10 ---- ==== ---- 16
7 E 5
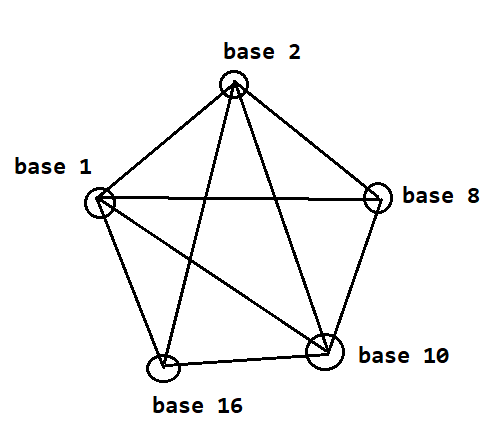
It is possible to convert directly between different numbering systems. If we use base 1, 2, 8, 10, 16 systems -- we should have 20 conversion rules.

To minimize the number of the necessary rules, lets morph our pentacle mesh into a star:
base 10
^
|
v
base 1 <---> (2) <---> base 8
^
|
v
base 16
Now we have only 8 rules (2 to 8, 8 to 2, 2 to 16, 16 to 2 are already explained. 1 to 2, 2 to 1 are obvious. So we have only two rules left).
Converting from binary to decimal
Converting from decimal to binary:
integer part
// integer part of the division
% reminder
a : b = { a // b, a % b }
:2 |
^
92 0
46 0
23 1
11 1
5 1
2 0
1 1
0
^
| result in this column, read from bottom to top
fractional part
|
*2 v
0.64 1.28
0.28 0.56
0.56 1.12
0.12 0.24
0.24 0.48
0.48 0.96
0.96 1.92
v
| result in this column, read from top to bottom
0.64 = 0.1010001... = 0.5 + 0.125 + ...
Build all eight converters explained
a : b = a // b, a % b
:2
92 0
46 0
23 1
11 1
5 1
2 0
1 1
0
*2
0.64 1.28
0.28 0.56
0.56 1.12
0.12 0.24
0.24 0.48
0.48 0.96
0.96 1.92
0.64 = 0.1010001... = 0.5 + 0.125 + ...
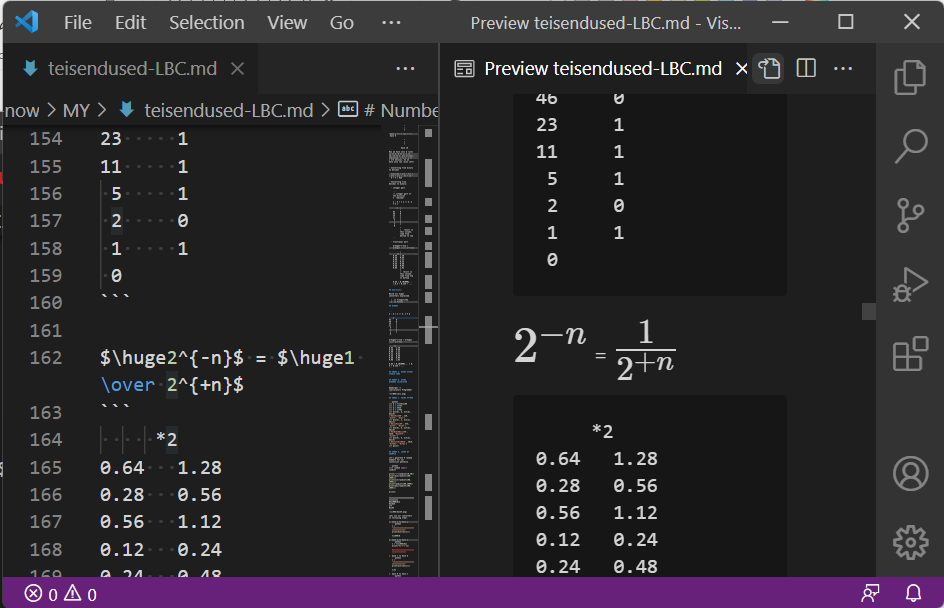
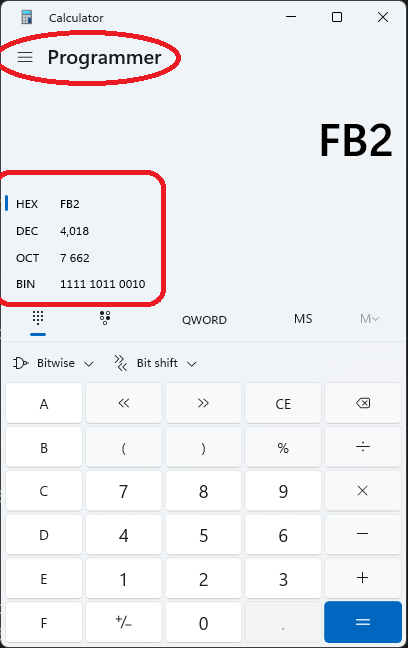
Hamburger -> [Calculator] Programmer
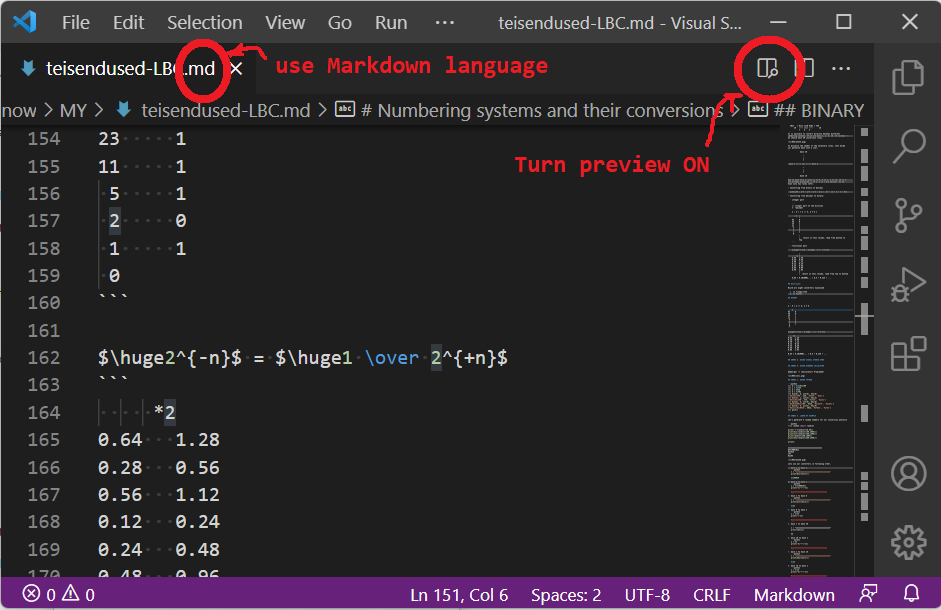
Thonny IDE (thonny.org) . In REPL window:
>>> b = 0b11011100
>>> o = 0o734
>>> d = 5436
>>> h = 0xFB2
>>> bin(b), b, oct(b), hex(b)
('0b11011100', 220, '0o334', '0xdc')
>>> bin(o), o, oct(o), hex(o)
('0b111011100', 476, '0o734', '0x1dc')
>>> bin(d), d, oct(d), hex(d)
('0b1010100111100', 5436, '0o12474', '0x153c')
>>> bin(h), h, oct(h), hex(h)
('0b111110110010', 4018, '0o7662', '0xfb2')
>>> quit()
Let's generate 5 random numbers for our conversion pentacle
from random import randint
print("1"*randint(10,50))
print(bin(randint(100,1000)))
print(oct(randint(100,1000)))
print(randint(100,1000))
print(hex(randint(100,1000)))
prints:
1111111111111111111111111111111111
0b110001011
0o1625
177
0x193

Lets use our converters in following order.
n = "1111111111111111111111111111111111"
print(bin(len(n)))
0b100010
n = 0b110001011
print("0u"+"1"*n)
0u1111111111111111111111111111111111
n = "1111111111111111111111111111111111"
print(oct(len(n)))
0o42
n = 0o42
print("1"*n)
0u1111111111111111111111111111111111
n = "1111111111111111111111111111111111"
print(len(n))
34
n = 34
print("0u"+"1"*n)
0u1111111111111111111111111111111111
n = "1111111111111111111111111111111111"
print(hex(len(n)))
0x22
n = 0x22
print("0u"+"1"*n)
0u1111111111111111111111111111111111
n = 0b1101001011
digit = ["000", "001", "010", "011",
"100", "101", "110", "111"]
s = "0" * (3-len("{0:b}".format(n))%3)+"{0:b}".format(n)
print("given:",s)
for i in range(0,len(s)//3):
slice=s[i*3:i*3+3]
for k in range(0,8):
if(slice==digit[k]):
print(digit[k],k)
# create list of digits
digit = ["000", "001", "010", "011",
"100", "101", "110", "111"]
for i in range(0,8):
if ("010" == digit[i]):
print(i)
# TODO
# TODO
n = 0b1101001011
digit = ["0000", "0001", "0010", "0011",
"0100", "0101", "0110", "0111",
"1000", "1001", "1010", "1011",
"1100", "1101", "1110", "1111"]
s = "0" * (4-len("{0:b}".format(n))%4)+"{0:b}".format(n)
print("given:",s)
for i in range(0,len(s)//4):
slice=s[i*4:i*4+4]
for k in range(0,16):
if(slice==digit[k]):
print(digit[k],hex(k)[2])
digit = ["0000", "0001", "0010", "0011",
"0100", "0101", "0110", "0111",
"1000", "1001", "1010", "1011",
"1100", "1101", "1110", "1111"]
for i in range(0,16):
if ("010" == digit[i]):
print(i)
base2to10(base8to2(n))
base2to8(base10to2(n))
base2to16(base8to2(n))
base2to8(base16to2(n))
base2to16(base10to2(n))
base2to10(base16to2(n))
n = 0b11011110101010
def base2to16(n):
digit = ["0000", "0001", "0010", "0011",
"0100", "0101", "0110", "0111",
"1000", "1001", "1010", "1011",
"1100", "1101", "1110", "1111"]
s = "0" * (4-len("{0:b}".format(n))%4)+"{0:b}".format(n)
print("given:",s)
for i in range(0,len(s)//4):
slice=s[i*4:i*4+4]
for k in range(0,16):
if(slice==digit[k]):
print(digit[k],hex(k)[2])
base2to16(x)
z = "1101001011"
def binstr2dec(x):
lenx = len(x)
summa = 0
for i in range(0, lenx):
a = int(x[i])
b = 2 ** (lenx - i - 1)
summa += a*b
print(a, "*", b, "=", a*b)
print("------------\n =", summa)
binstr2dec(z)